[太阳黄经多少度算正常范围]太阳直射点纬度与时间的关系曲线及其应用
这首诗的文本最早是在我高三升学军事训练(2019年9月)午睡备考初中地理时的一些意念,在一段日数的思索后确实斩获了不少的科学知识:
高三上学年独立发现了阳光普照日数排序式子(该片该文未提到,但听众可以很容易地推论),月亮天樽二与分点的换算成式子,第谷方程组(欧几里得法),并自学了三角学此基础;后来高呵呵学年对数学分析、数学分析等数学分析有了一定的此基础后,推论出了日数关于分点的点数表示;高二上学年了解到了Bessel函数得出的第谷方程组级数解;Chhatarpur学年的一场碰巧有兴趣利用它来排序幼儿园旁边山的落差....
初中这么几年来反复思索这个研究课题,以致这首诗也更新了很多次,该文质量自然也骤然不断上涨。这首诗首秀于禽流感期间(2020年4月),之后在2021年1月有过大的更新。这次(22年元月)也是一场更新,带入了很多捷伊文本,主要包括呵呵文本:
行星测绘学的进阶基本概念第谷三运动定律的推论第谷方程组量测幼儿园旁边山的落差
刚进入初中的时候,在扁果上自学了月亮照射到点经度的基本概念,老师的ppt上出现了近似于这样的一张图片:
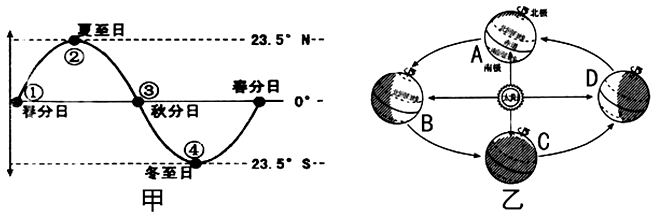
 月亮照射到点的重回体育运动
月亮照射到点的重回体育运动
我就较为疑惑这函数抛物线的函数会是怎样的( ̄▽ ̄)",毕竟当时上课时也正在自学函数嘛,看到函数影像老想着T5800函数(●ˇ?ˇ●)
何不设月亮照射到点层次记为 (以下均称为月亮赤纬),以秋分日起的日数记为 ,所以该图相关联的函数即为 。
既然要排序 ,所以就得认知 为什么要随着日数 变化,对吧?\( ̄︶ ̄*\))
在扁果上我们自学到:由于地球绕月亮太阳,这会导致月亮照射到点在南北重回线上重回体育运动,其体育运动周期为一个重回年[1]。
为了较为好认知为什么月亮照射到点会在南北重回线之间体育运动,我们何不引入几个简单的基本概念:
天球[2]:一个与地球同球心,并有相同的自转轴,半径无限大的球。天空中所有的物体都可以当成投影在天球上的物件。
天赤道:地球赤道在天赤道上的投影,为一个大圆。
天极:地球南北极点在天球上的投影。
黄道:一个重回年,地球太阳轨道在天球上的投影,为一个大圆。
升降交点:天赤道与黄道的交点,存在两个交点。月亮在天球上的投影由南天球体育运动到北天球经过的升降交点称为升交点(又称秋分点,符号为 );月亮在天球上的投影由北天球体育运动到南天球经过的升降交点称为降交点(又称秋分点,符号为 )。
可以参照下图1来认知这几个基本概念
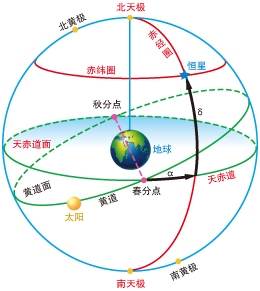
图1 图源自百度
相信你已经认知它们的意思了吧||ヽ(* ̄▽ ̄*)ノ,既然认知了那就重新回到我们的思路。我们现在的目的是认知:为什么一个重回年中,月亮照射到点会在南北重回线之内重回体育运动?
既然黄道是地球太阳轨道在天球上的投影,所以根据相对体育运动,月亮在天球上的投影一定也位于黄道上(可以参考上图),对吧?()?。所以地球在一个重回年中绕月亮太阳,相关联的就是月亮在天球上的投影沿着黄道体育运动一周。
所以不难思索:月亮在天球上的投影(即月亮照射到点)在一个重回年中是沿着黄道自西向东体育运动一周的。
其中与黄道相切的两个平行于天赤道的小圆就称为南北重回线,所以在一个重回年中月亮照射到点会在南北重回线之内重回体育运动。是不是很好认知呢!(*≧︶≦)
既然月亮照射到点(呵呵简称为点 )会体育运动,所以现在我们就有必要引入坐标来描述它的体育运动了。球面上最常见的坐标莫属经经度了:
在天球上,以秋分点为坐标原点,沿着天赤道取经度(称为天樽二) ,向东为正,向西为负;垂直于天赤道取经度(称为赤纬) ,向北为正,向南为负。
地理教科书又告诉我们,黄道和天赤道的二面角称为黄赤交角,其数值 ,且南北重回线为于平行于天赤道并于黄道相切的小圆,所以可见南北重回线的赤纬自然就是 。
而点 的体育运动是沿着黄道自西向东的,所以我们只需要知道 与秋分点 关于天球球心 的夹角 (如下图2)即可完全掌握 的体育运动。
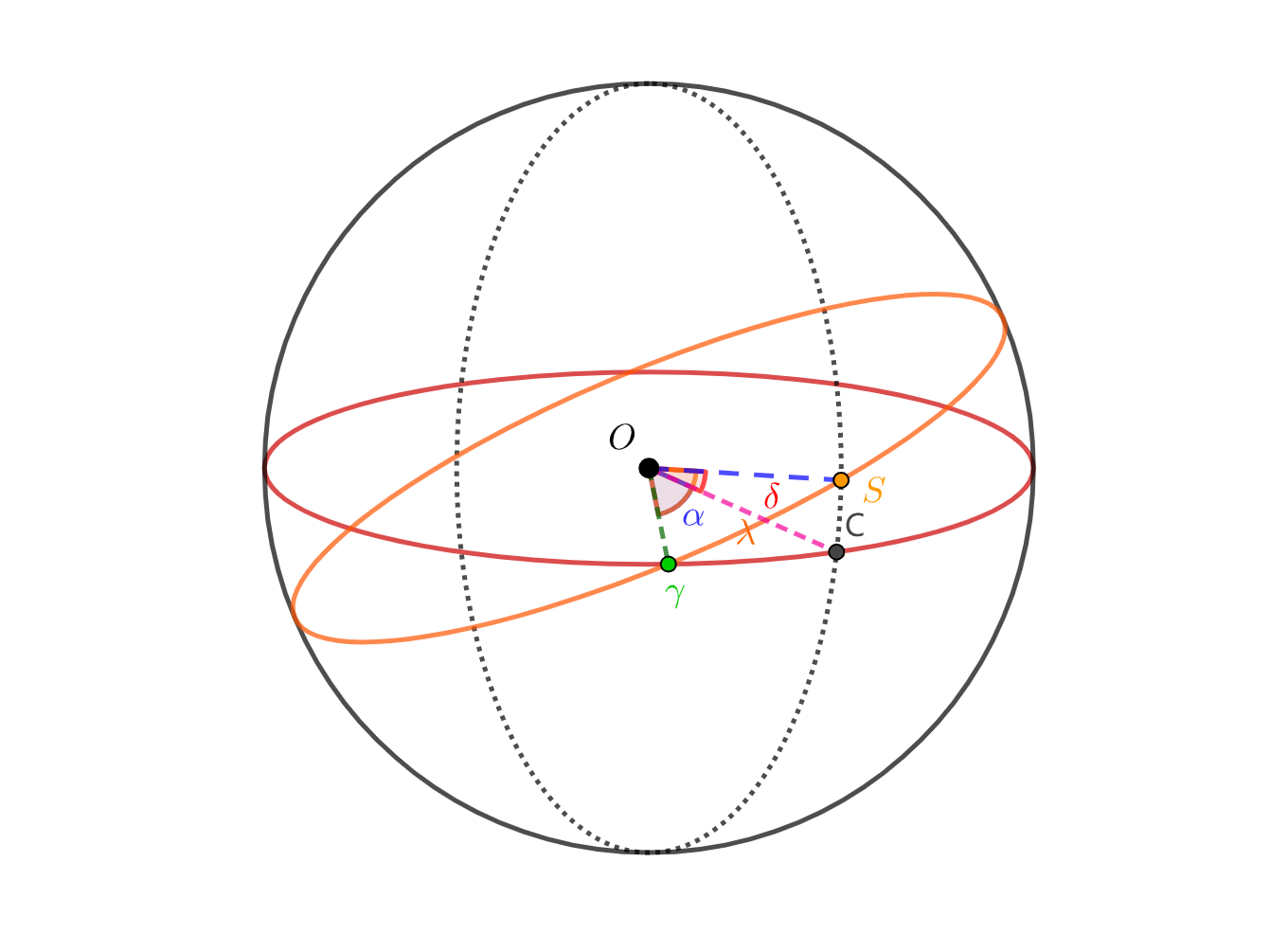
 图2 Geogebra绘制(后同)
图2 Geogebra绘制(后同)
显见 是关于 的一个单调函数 。且根据球面上一点欧几里得关系,可以确定 与 的换算成关系。所以为求得 ,我们得先求得 与 的换算成方程组,以及 。
参照图2,我们可以以点 为原点,天赤道所在平面为 平面,射线 为 轴正方向建立右手系 。(如下图3)
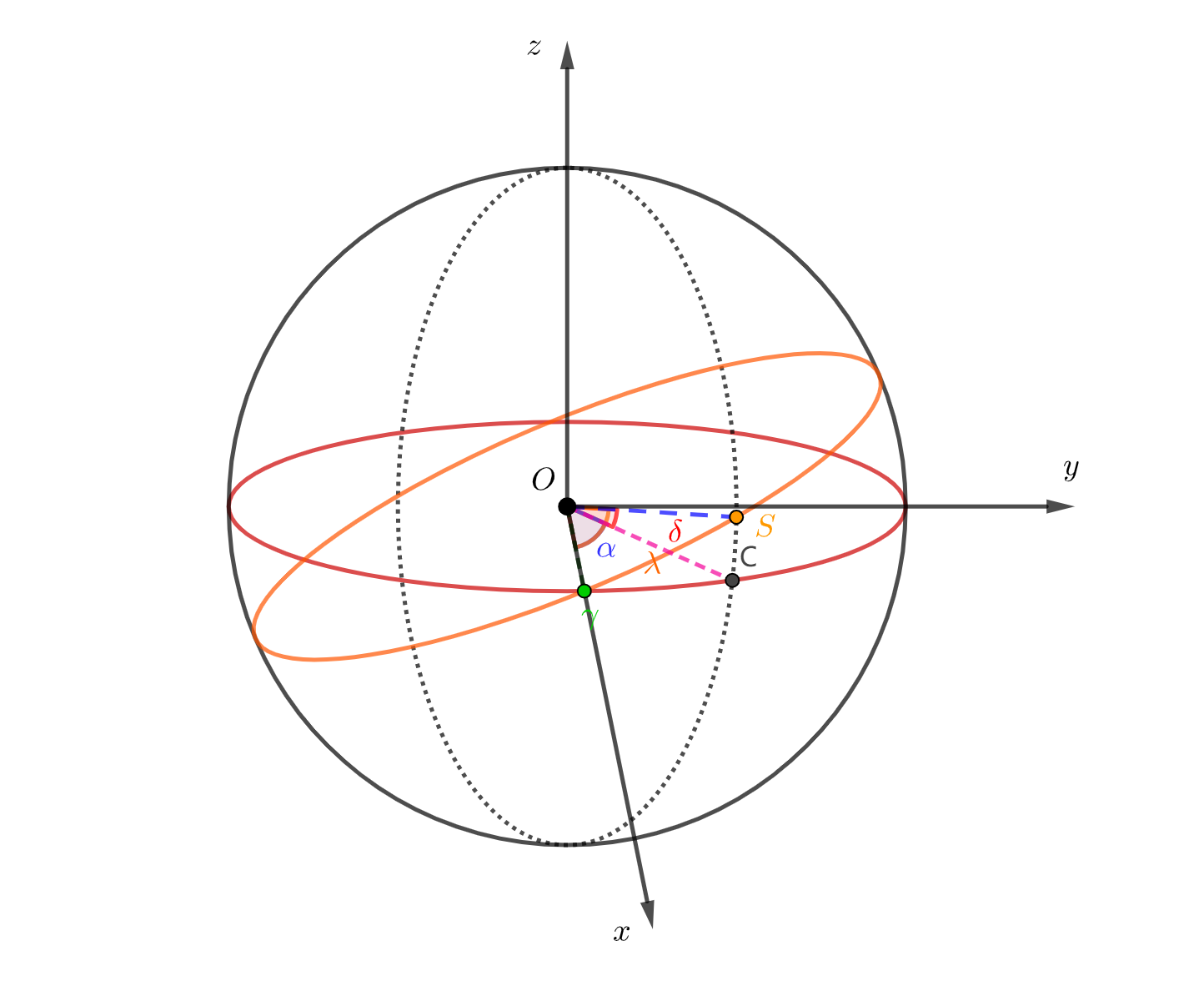
 图3
图3
因为我们研究的问题是天球上的投影,与天球本身半径并无关系,所以为简便运算,何不定义天球的半径为单位 。
考虑坐标变换:使 轴绕 轴逆时针旋转 ,得到捷伊坐标系 ,使得 轴垂直于黄道面。所以自然有:
于是我们得到:
对式子(1)同乘一个 后有:
再将式子(2)代入此式得:
所以我们得到了 的换算成方程组[3]:
接下来就还剩下求解 的问题了。
//马上要进入物理领域了哟,同学们系好安全带// (/▽\)
注意到 这个角度与地球绕月亮太阳的径角是相等的,如图4所示
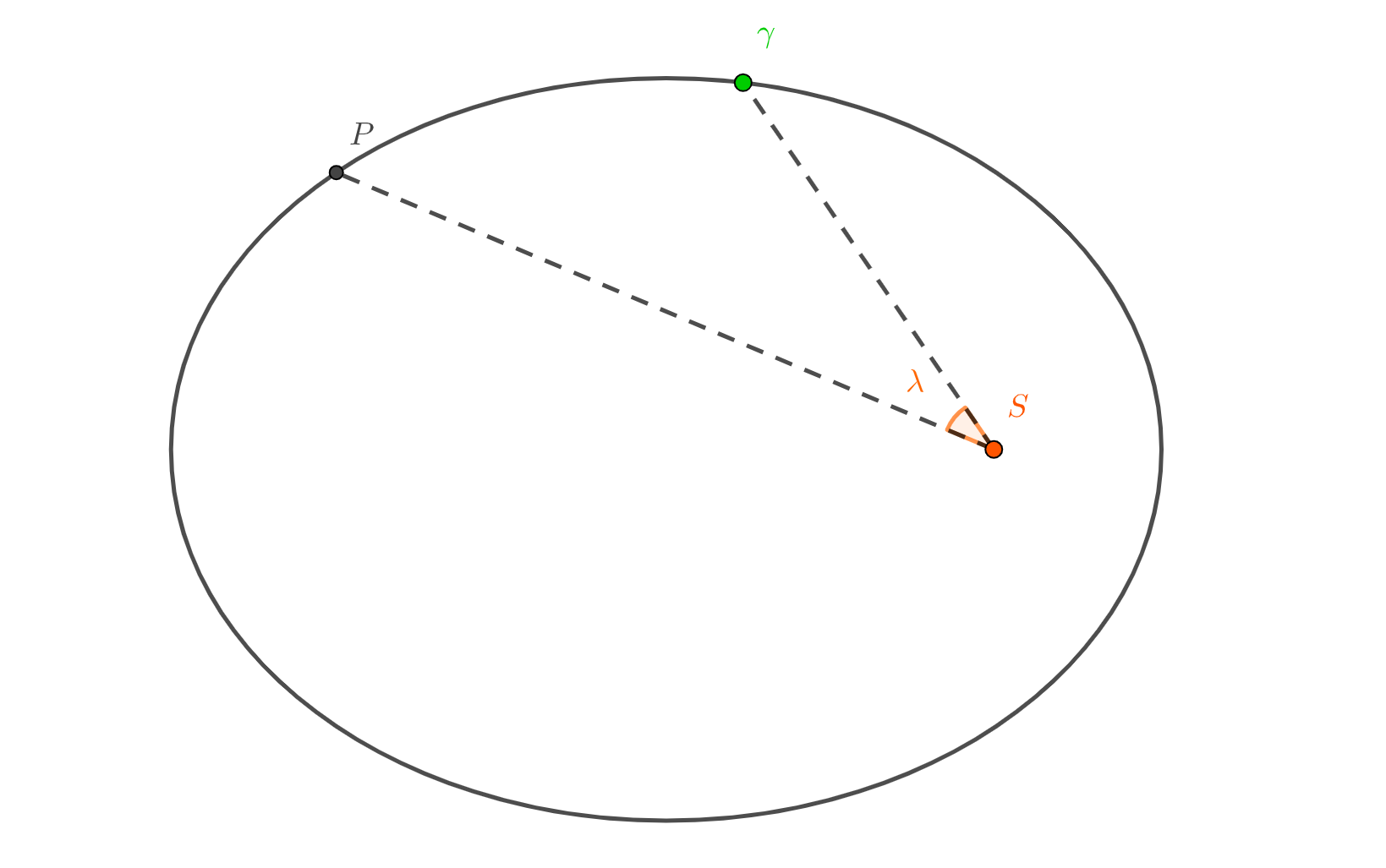
 图4 其中γ代表秋分日地球经过地点,P代表地球所在位置,S代表月亮
图4 其中γ代表秋分日地球经过地点,P代表地球所在位置,S代表月亮
可见,想要求得 ,不牵扯到万有引力或者第谷运动定律是不可能的了。
第谷第二运动定律无非是一个角动量守恒,作图如下:
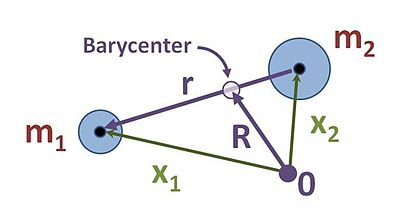
图源自百度
取空间内一点 作为参考点,定义月亮(质量为 )、地球(质量为 )的位矢分别为 ,且
我们可以发现,若以月亮为参考系,所以有:
我们可以定义如下守恒量
这是万有引力为有心力[4]的必然结果。在此守恒量的此基础上,很容易导出第谷运动定律,不想了解第谷运动定律如何推论的也不要紧,只需知道下文式子(*)为一个守恒量即可跳过呵呵选读文本[5]:
取极坐标 ,极点为 ,极轴为近日点所在椭圆长轴射线。可以定义两个正交归一基底[6]:
再取一平面直角坐标系 ,原点位于 , 正半轴与极轴相同,同样可以定义正交归一基底:
所以根据基底变换式[7]:
我们可以将极坐标基底展开为直角坐标基底:
所以求导有:
排序
显然在已确定的地球轨道(即已知长半轴长 以及离心率 )上,地球质量 对 的是没有任何影响的。由此,根据上式(4)我们何不定义一个捷伊守恒量:
(1)第谷第二运动定律:
(2)第谷第一运动定律[8]:
对引力加速度(定义 与 做叉积有
所以我们可以定义一个守恒量,称为:
再将该矢量与 点乘有:。
(3)第谷第三运动定律:
对比椭圆极坐标方程组以及轨迹方程组,自然有下式成立:
既然地球的体育运动轨迹为椭圆,所以结合第二运动定律可以知道有如下方程组成立:
其中 为一个恒星年, 代表椭圆面积。所以可以验证:
其中第二个等号用到式子(6)。
注意到 与 实际上只相差一个常数 :
这个 就是秋分日地球所在位置相关联的极角(图4中点 的极角),目前它大约为 。
为排序 只需要排序 即可。注意到守恒量 含有 ,可以考虑分离变量点数(不要忘记把日数单位制换为日数,弧度制改为角度制哦~):
其中用到椭圆方程组以及式子(7)。
可见,式子(3)和式子(8)即为 抛物线的参数方程组。由参数方程组绘制 抛物线如下:
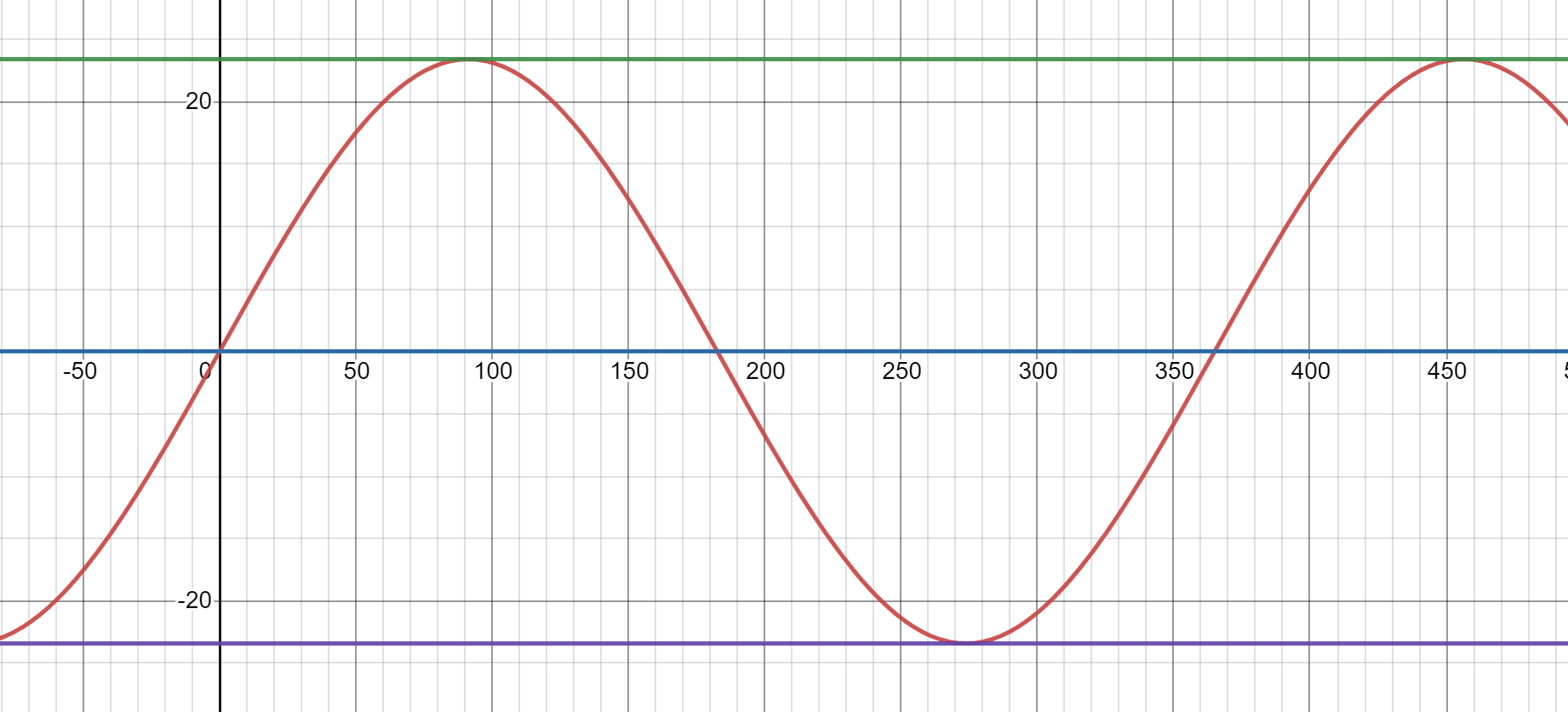
 图5 月亮照射到点经度关于日数的函数影像(节选) 图源自Desmos
图5 月亮照射到点经度关于日数的函数影像(节选) 图源自Desmos
虽说是把参数方程组得到了,但想要得到 的函数还是需要较为强的数学能力,下面说明呵呵:
首先解决点数:
所以根据式子(8),若令
则有:
此时令
自然有
所以得到了椭圆形式的[9]:
想要求得 只需求解该方程组即可(我的能力到这了...( _ _)ノ|),得到 后代入式(3)即可得到 。至于第谷方程组的解析解有很多种形式的,下面这首诗总结了很多,大家感兴趣可以阅读呵呵:
其中我个人较为喜欢贝塞尔级数解结合多重对数函数得到的的取整点数形式[10]:
酱紫君的文中提到到的这篇文献()更是将 的定义延拓至复数集,得出了更一般的解法,这篇知乎回答[11]也给该论文得出了详细讲解:
月亮高度 在一天中达到最大值时称月亮上中天(正午),达到最小值时称月亮下中天(子午)。
对于非地球两极的观测点,我们称过两次中天月亮所处位置的天球上的大圆称为子午线。子午线与地平线的交点为南北点,靠近北方的点称为北点,靠近南方的点称为南点。
过行星所在位置和天顶的半大圆与地平线的交点到北点的大圆弧度称为该行星此时的方位角 。
由坐标 刻画行星位置的坐标系就称为地平坐标系。如下图:
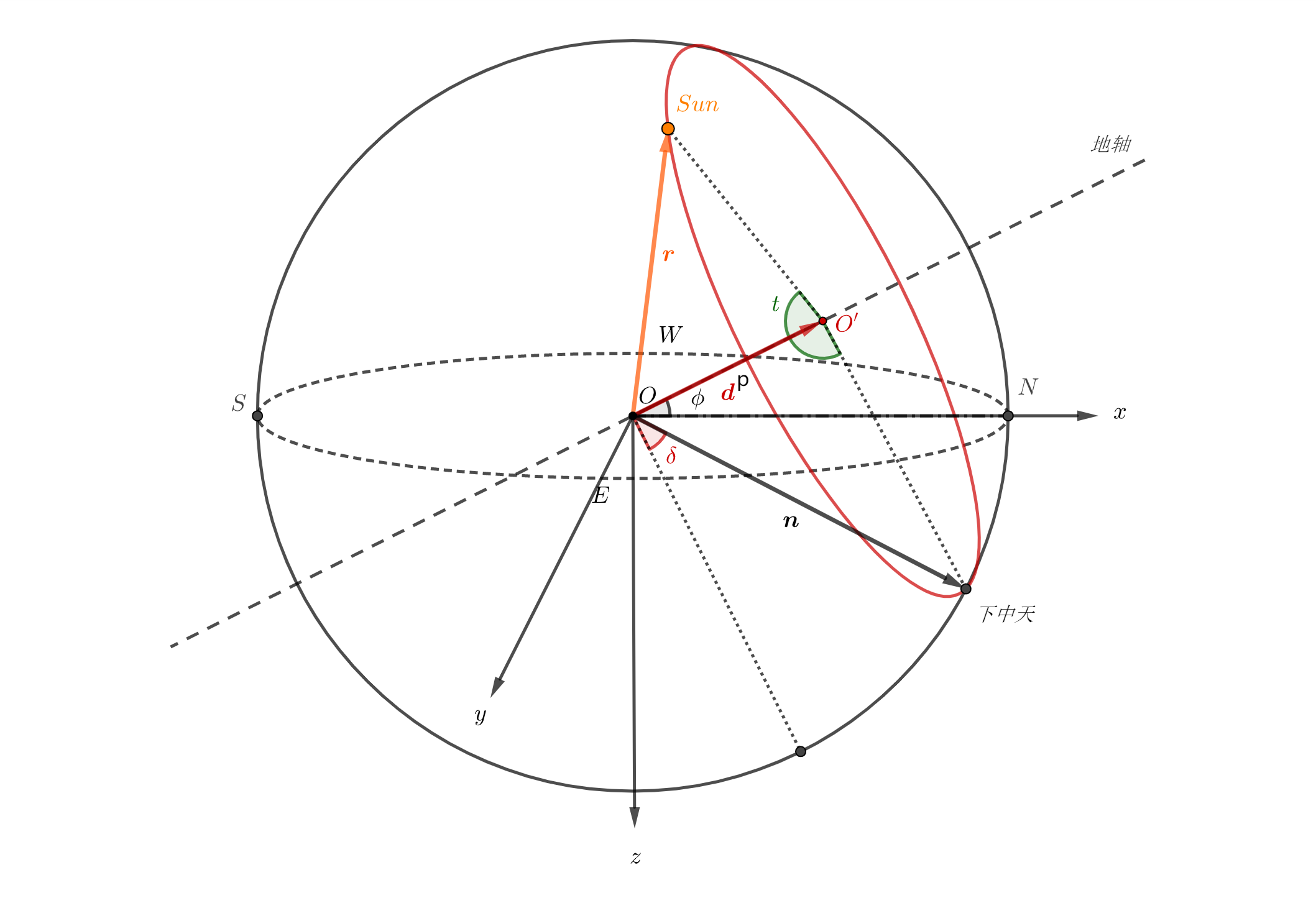
 图6 地平坐标系与月亮周日视体育运动示意图,以夏季北半球中经度为例
图6 地平坐标系与月亮周日视体育运动示意图,以夏季北半球中经度为例
其中地理经度为 ,角度 称为时角。空间直角坐标系 原点位于天球圆心,沿正北方位 轴正方向,正东方为 轴正方向,天底方向为 轴正方向建立。 为月亮位矢, 为下中天位矢, 为月亮视体育运动轨迹圆的圆心位矢。
所以在此直角坐标系下各向量可表示如下:
所以可以排序:
所以我们得到了方程组组:
消去方位角 得:
解二次方程组得
由于 时分别代表月亮下中天和上中天,即 取的最小值和最大值,则 取负。即: 式(12)即可使我们排序月亮高度,而对于月亮方位角,只需对方程组组(11)中的第一个方程组变呵呵形即可:
先介绍呵呵我幼儿园周围的环境吧。
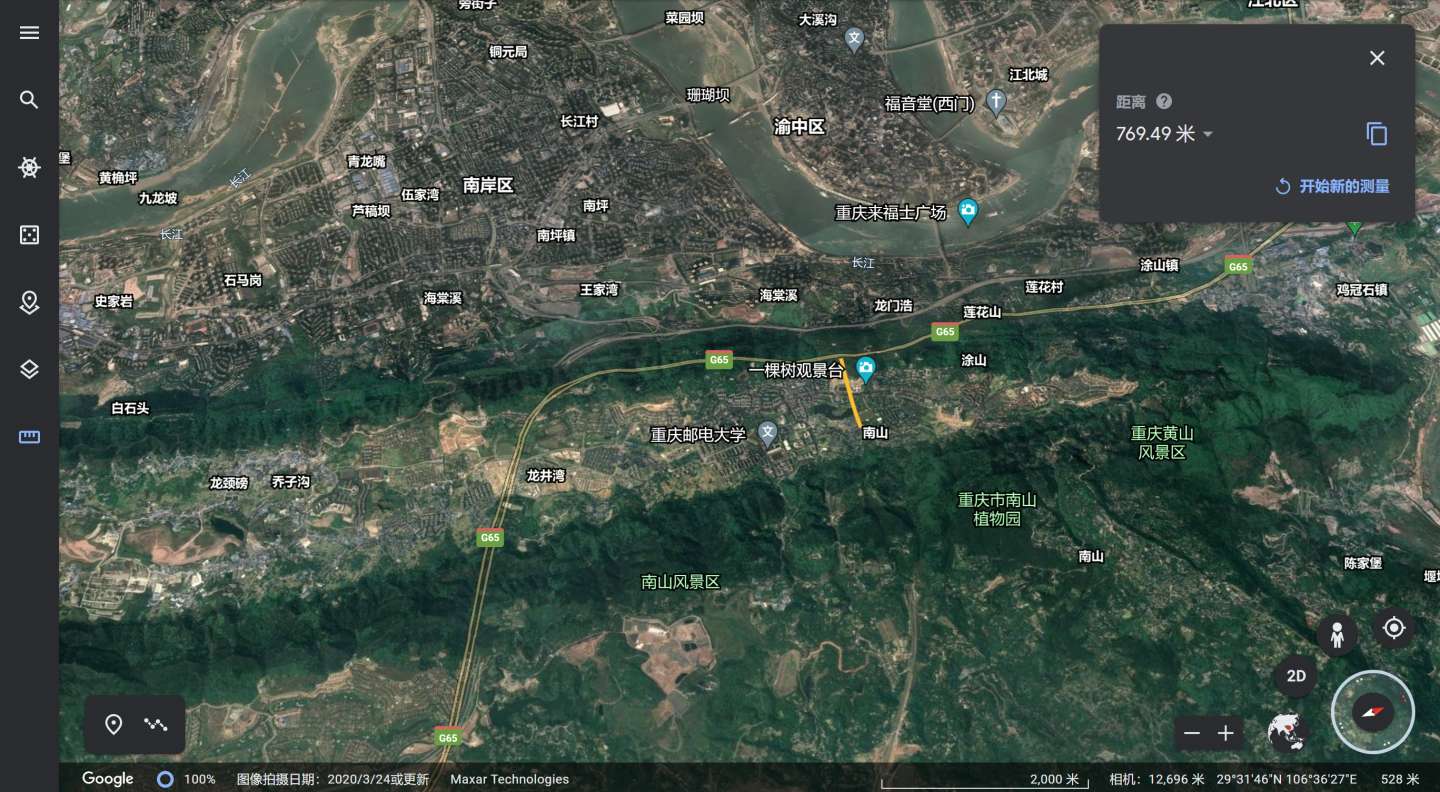
 图7 幼儿园附近区域鸟瞰图(黄线一端是待测山脉,另一端为幼儿园教学楼所在地),此图向上大致朝西北,图片源自Google Earth(后同)
图7 幼儿园附近区域鸟瞰图(黄线一端是待测山脉,另一端为幼儿园教学楼所在地),此图向上大致朝西北,图片源自Google Earth(后同)
重庆第二外国语幼儿园[12]坐落于重庆市南岸区的南山山顶的一片背斜谷地[13]中央。地势中间低,东西两侧高,即幼儿园东西两侧是两端近乎平行的山脉,在俯瞰图中相关联 ""型的山岭。这次需要量测的主角就是""型的山岭更靠近两江的一侧山岭。如下图:
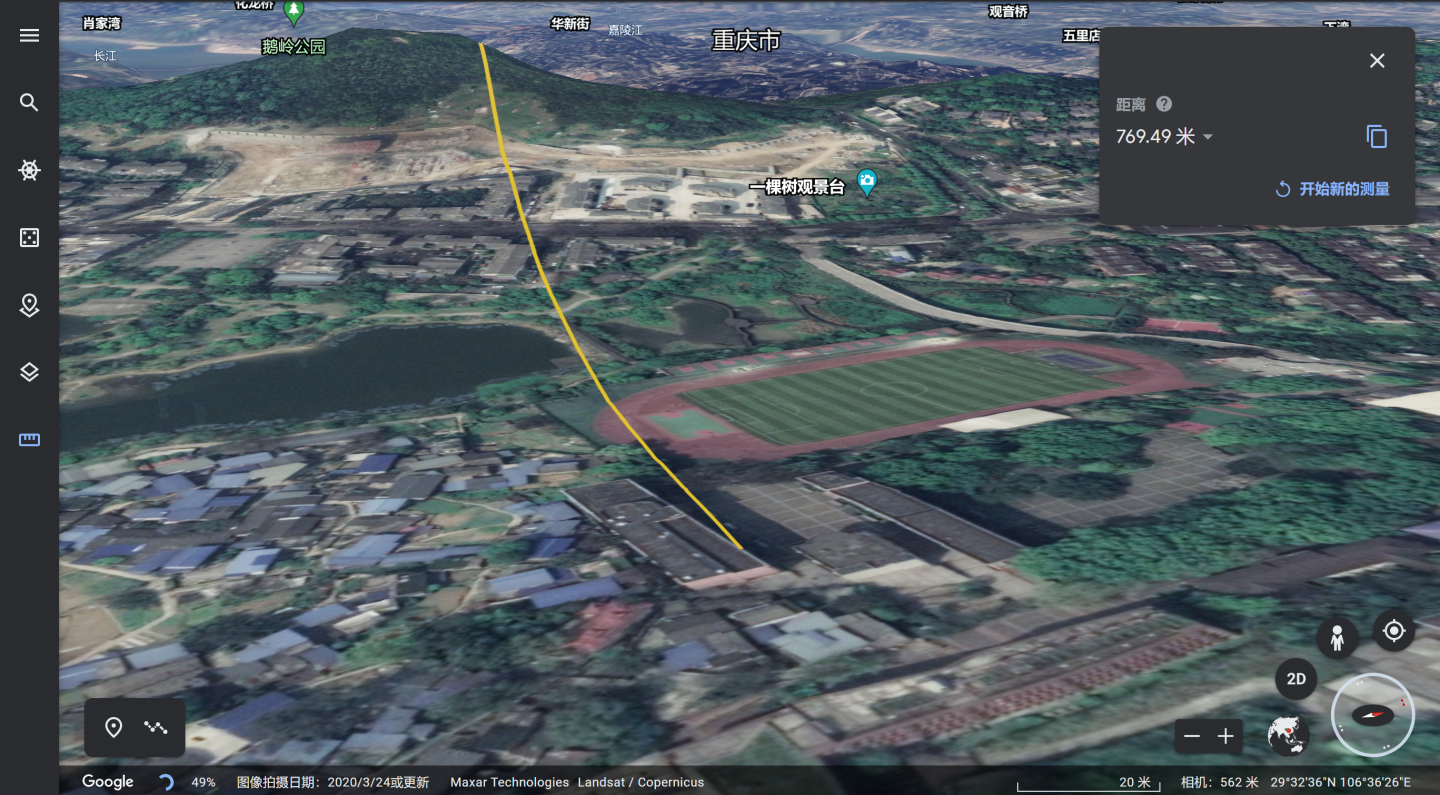
 幼儿园旁边小山岭的正视图
幼儿园旁边小山岭的正视图
实际景象呢可以参考呵呵图片:

 图片来源于我的地理老师(下同) 由于拍摄时期和我观测的时期不同,所以Google Earth上标记的日落点略有不同
图片来源于我的地理老师(下同) 由于拍摄时期和我观测的时期不同,所以Google Earth上标记的日落点略有不同



观测日数:2021年3月30日和5月28日傍晚;
观测地点:先后有两次观测,一场在幼儿园篮球场附近;一场在教室窗边(5楼);观测所需数据来源:观测地大致经经度:通过手表的GPS,获取幼儿园所在地大致经经度;落山时刻月亮的方位与高度:先后有两次在不同地点观测月亮日落,并记录下手表上显示的日数。然后通过前文所撰写的文本来运算出两次观测月亮的方位与高度;教室观测点到教学楼末端的长度:使用学生直尺量测教学楼一块地砖(正方形)的边长,并计数从教室门口到走廊尽头的地砖个数,从而得到观测点教学楼教室观测点到教学楼末端的长度;教室观测点到篮球场观测点的落差:由于教学楼下是平地,即篮球场与教学楼一楼等高,通过楼层数加上人的正常身高可排序出落差;教学楼朝向的方位角:通过"立笔见影"粗略测得(详情见后);数据处理方法:运用前文所撰写的科学知识以及一些简单的解三角形科学知识。
来看看两个观测地内部环境,如图:
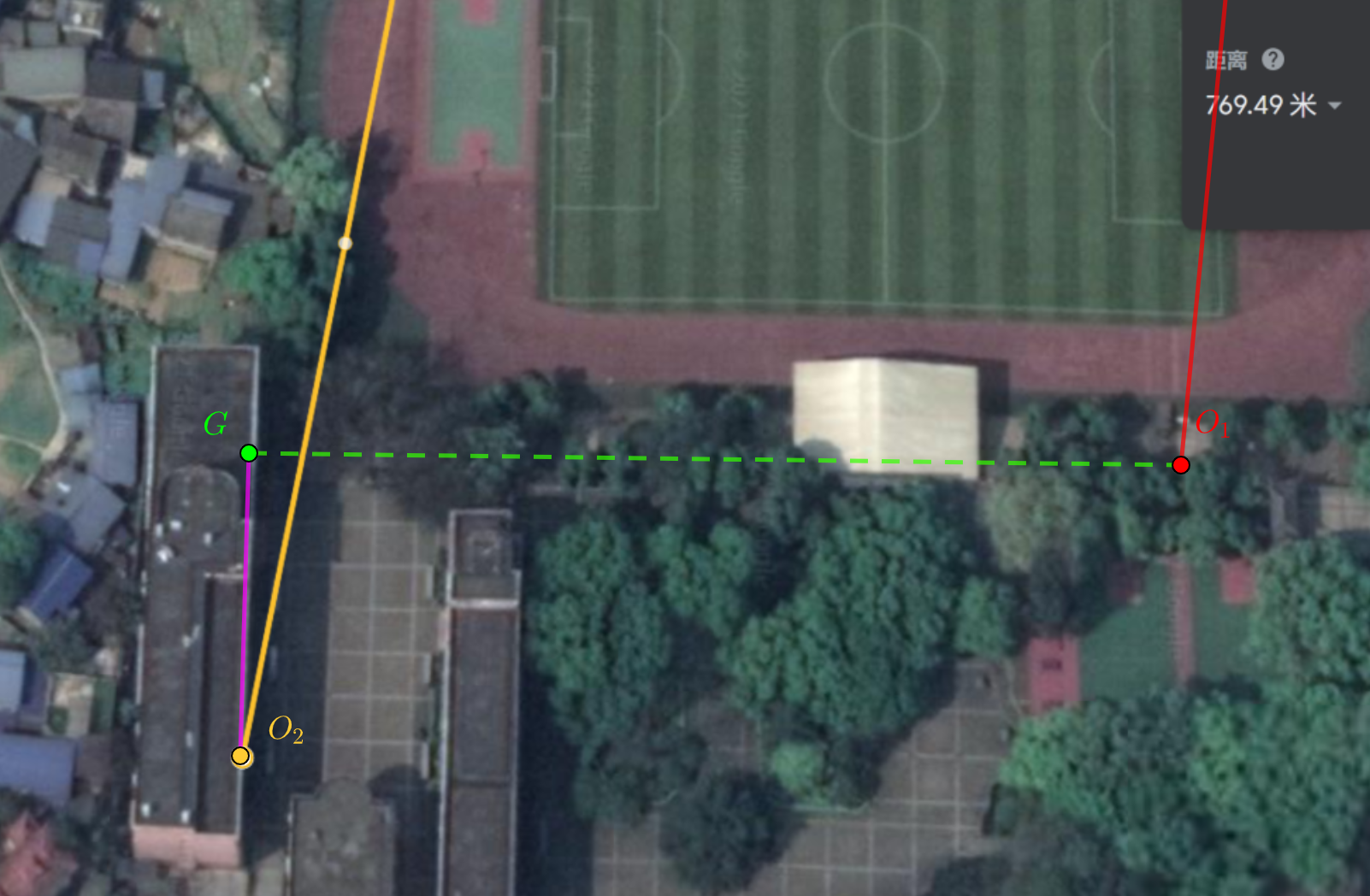
 图8 教学楼(O2)与篮球场(O1)周边鸟瞰图 点G为教学楼走廊尽头
图8 教学楼(O2)与篮球场(O1)周边鸟瞰图 点G为教学楼走廊尽头
为了简便运算,得假设几个条件:
被测山脉两次落山点的海拔相等
通过这两个假设条件,就可以把这个量测问题完全转化为数学排序题目了。作图如下:
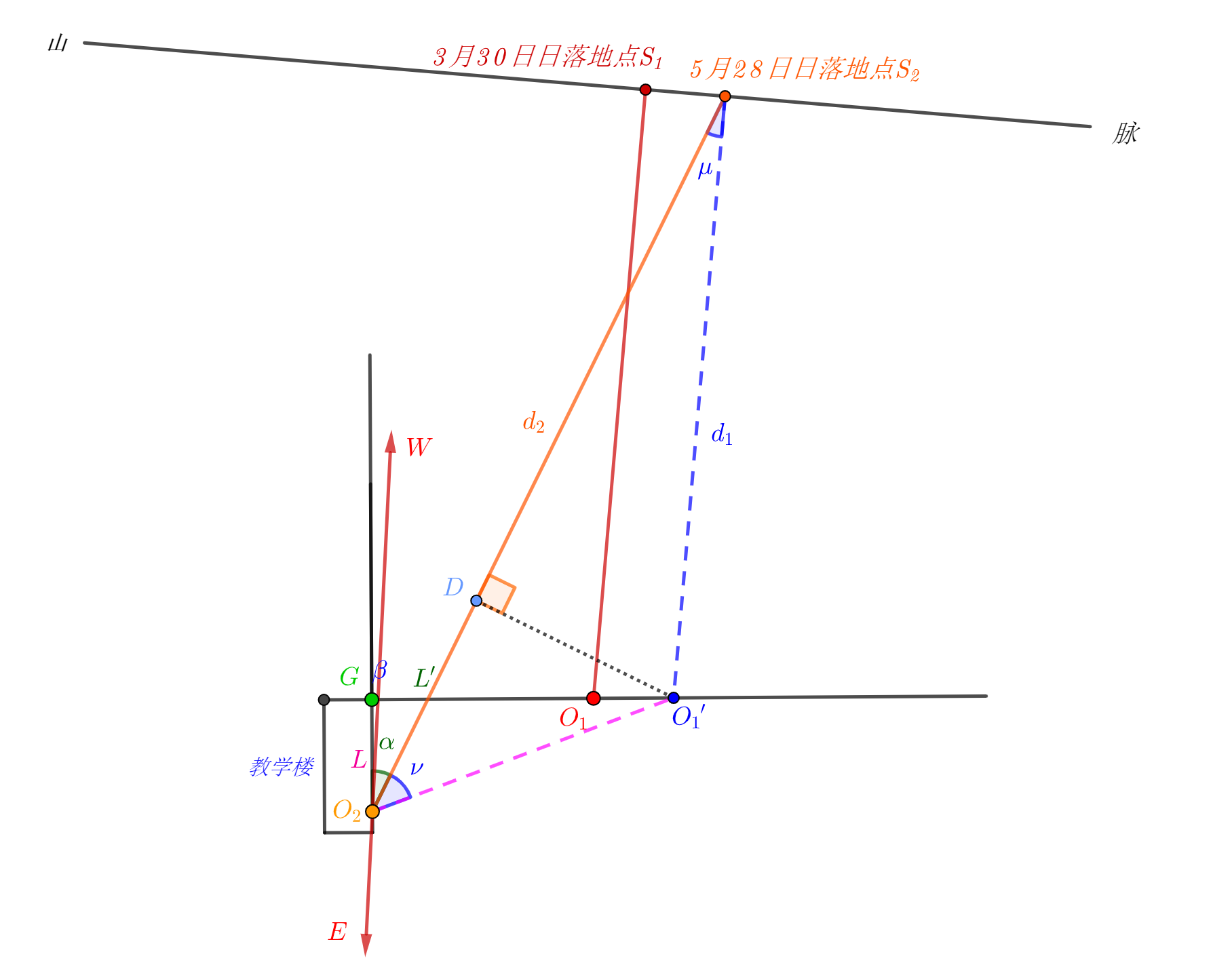
 图9 两观测地简图
图9 两观测地简图
根据幼儿园经经度 ;3月30日日落日数 ,5月28日落日数 ;按照前文文本排序出呵呵数据:
现在来排序图9中的角 。如图10:
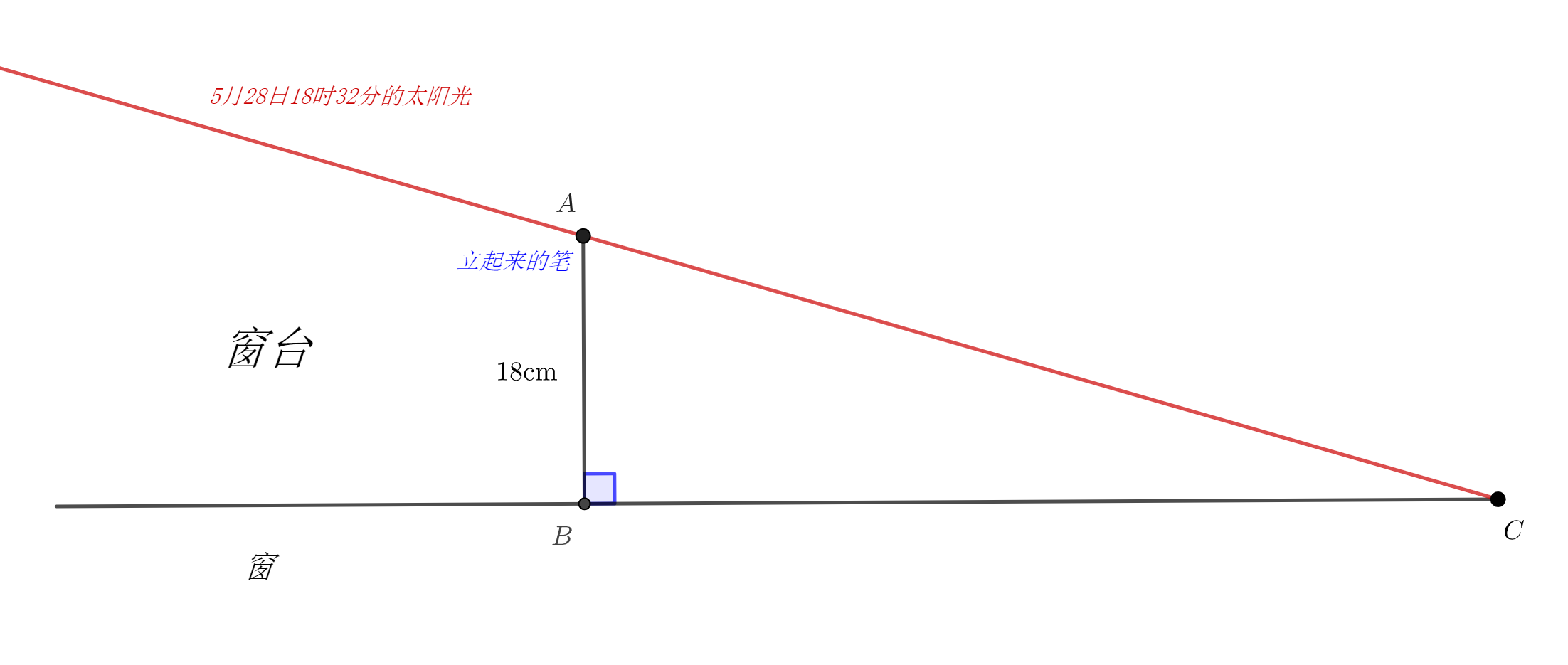
 图10 5月28日18时32分月亮光打在窗台上,通过"立笔见影"量测教学楼畅向方向角 俯视图
图10 5月28日18时32分月亮光打在窗台上,通过"立笔见影"量测教学楼畅向方向角 俯视图
用手扶着一支笔使其立在窗外的窗台上,控制好笔的位置使其影子尖端恰好位于窗户边缘 ,记录下此时笔的位置 。使用学生直尺测出点 到窗户的距离 ,以及笔的长度 。
由表可知,此时月亮高度 ,所以可知 ,进而有
由表可知,此时月亮方位角 ,即可排序得 ;
由表可知,当日日落方位角 ,结合 即可排序得图9中 ;
如图9,过点 作 平行线交 延长线为点 。由表可知3月30日日落方位角为 ,做差得图9中角 ;
设图9中 , 。过点 作 的垂线,垂足为点 ,记 。
由于 , ,故点 在以 为直径的圆上,如图11:
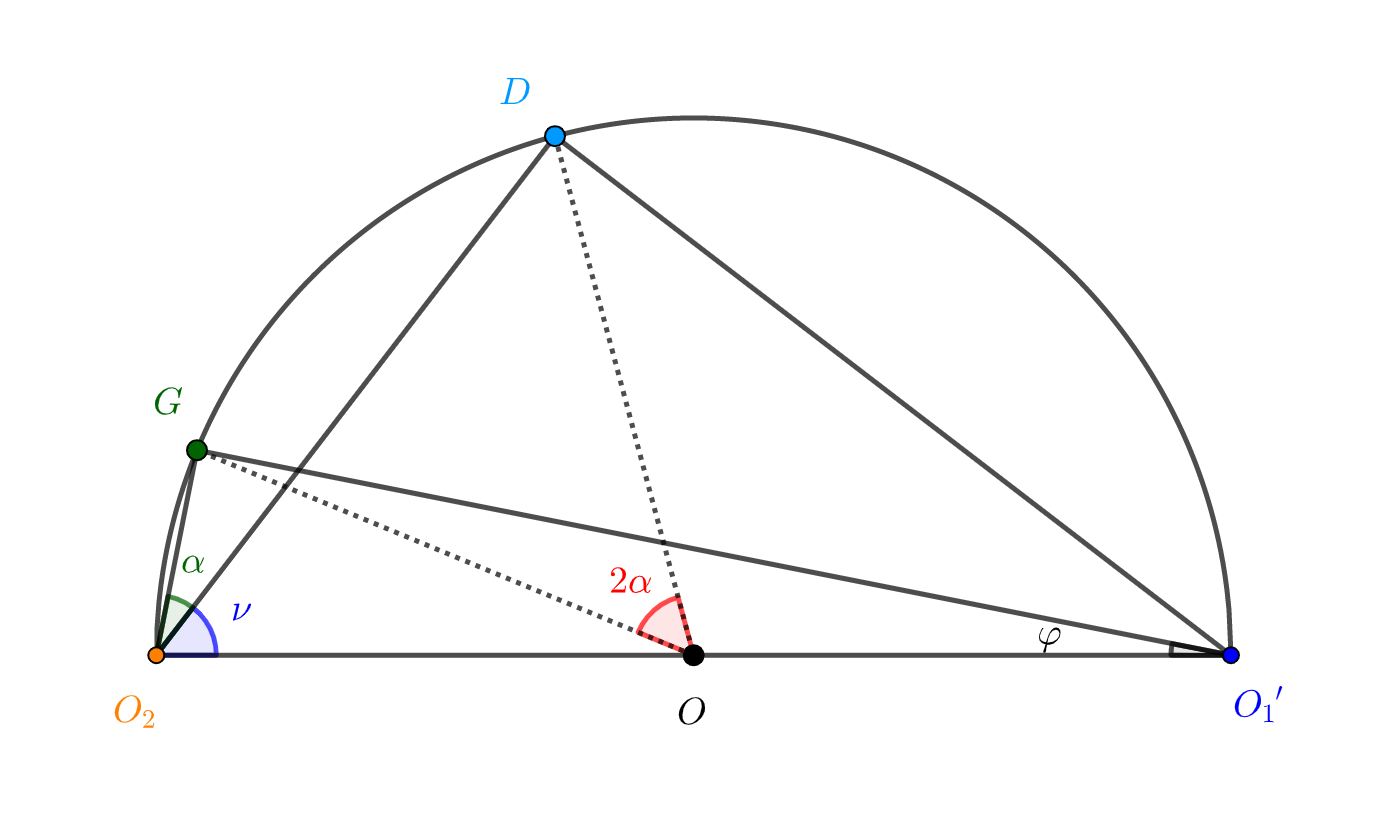
 图11
图11
其中点 为圆心,设 ,圆的半径为 。由圆周角定理显然得到 。
根据欧几里得关系有:
所以得到
如图9,设 。所以对于 ,有如下关系:
设两次落日时的月亮高度分别为 ,教学楼到篮球场的落差 ,所以在竖直方向上有:
联立式(14)(15)(16)整理得关于 的方程组:
由于教室位于五楼,考虑人身高大致为 ,一层楼大约高 ,所以有 ;
用学生直尺测出教室一块地砖(正方形)的边长为 , 计数 线段方向上一共有 块地砖,所以有 ;
根据表格,有 。将以上数据代入方程组(17)解得 ;
再将 代回式(14)(15)得 ;故山顶到篮球场的落差为
大功告成!!!
用谷歌地球试了呵呵,它得出的 大约为七百多米,比我算出来的数据小了不少,看来量测误差还是蛮大的,想了想,大概误差主要是 角 ,落差 ,走廊长 带来的吧。怎么说,至少知道那座山的落差在 之间[]~( ̄▽ ̄)~*。
好了,这篇更新了不少次的该文,也是我来知乎写的第一首诗,就到此吧!感谢阅读!
推荐阅读
-

?宝马新5系配置详解!这17款车型你最想入手哪一个?
-
黑龙江省290农场一天比一天热这钱真不好挣是用汗水换来的哎
{{if!data.isVip&&data.isActText}}{{elseif!data.isVip...
-
黑龙江干流堤防290农场段再次出现溃口
本报记者从吉林省水利厅水利厅司令部了解到,继16日再次出现宁远河后,27日7时,吉林河段堤防290农庄段悲剧重演宁远河。历经三个多...
-
黑龙江农险冰火两重天地方财力不足致补贴不一|农业保险|农险|财力
位于中俄林密吉林沿线的集贤县五原镇东方村今年遭遇洪水侵袭,许多农农作物受灾地区,农民周俊民种的200亩小麦几乎无人问津。幸好他参与...
-
黑龙江农垦290农场大雁繁育基地成为湿地生态养殖亮点
【编者按·中国军用养殖业网】日前,农牧一八〇农庄红树林自然保护区不远处,1500万头毛发亮光、身形丰满的雁在大坑里无拘无束地玩耍,...
-
鲜为人知的“料罗湾海战”——晚明与荷兰的战争
事件起因国内背景明崇祯时期,受小冰河期影响。中国北方长年干旱、中原和东部数次特大地震、北方瘟疫流行。除江浙闽粤一带受灾影响后仍然恢...
-
魏县关于进一步调整疫情封控管控措施的通告
肥乡县禽流感防控工作工作组办公室关于更进一步修正禽流感封控管控举措的通告各阶层农村居民:为统筹推进禽流感防控工作和经济社会发展,...
-

高职高考2022年可报考院校及最低录取分数线
-

高尿酸常常没有症状尿酸高可致痛风肾病和结石
-
高一学生举报老师教师节强制收礼:教师节,你准备送礼吗
立刻就要到此日了,每月那个时期,小学生家长们都心里感到恐惧,特别是新升学的小孩小学生家长,不晓得要千万别给同学赠礼,也不晓得新幼儿...

