[六点后太阳一定在正东方向吗]地理中的数学(太阳视运动)

前两天上午2点多的这时候在出租车上，丈夫和我说，后面小车的另一面是朝东偏的，我一看还啊。尽管偏的不多，但的确是偏东(匝道是南北向因此很明显)。这表明月亮是在偏东路径。自述初中的科学科学知识，应该只有月亮照射到点以南的地区才会看见月亮在北方。马上查了下广州的经度：22.5°N，的确在赤道(23.5°N)以上，但现在已经是7月23日了，距月亮最南的这时候(冬至6月21日)都过去了三个月了，月亮也该往南挪个6°,7°了吧，照射到点的确在广州以南了。那是咋呢？

丈夫打趣说，何况火星前段时间没有在太阳，因此前段时间这么多灾害！我揣测，呢路不是平的，因此看上去另一面朝东？但即便还是不确认原因。为了给小学生作出把科学知识用于生活的好榜样，我发了贴文(也是希望谋求标准答案)。

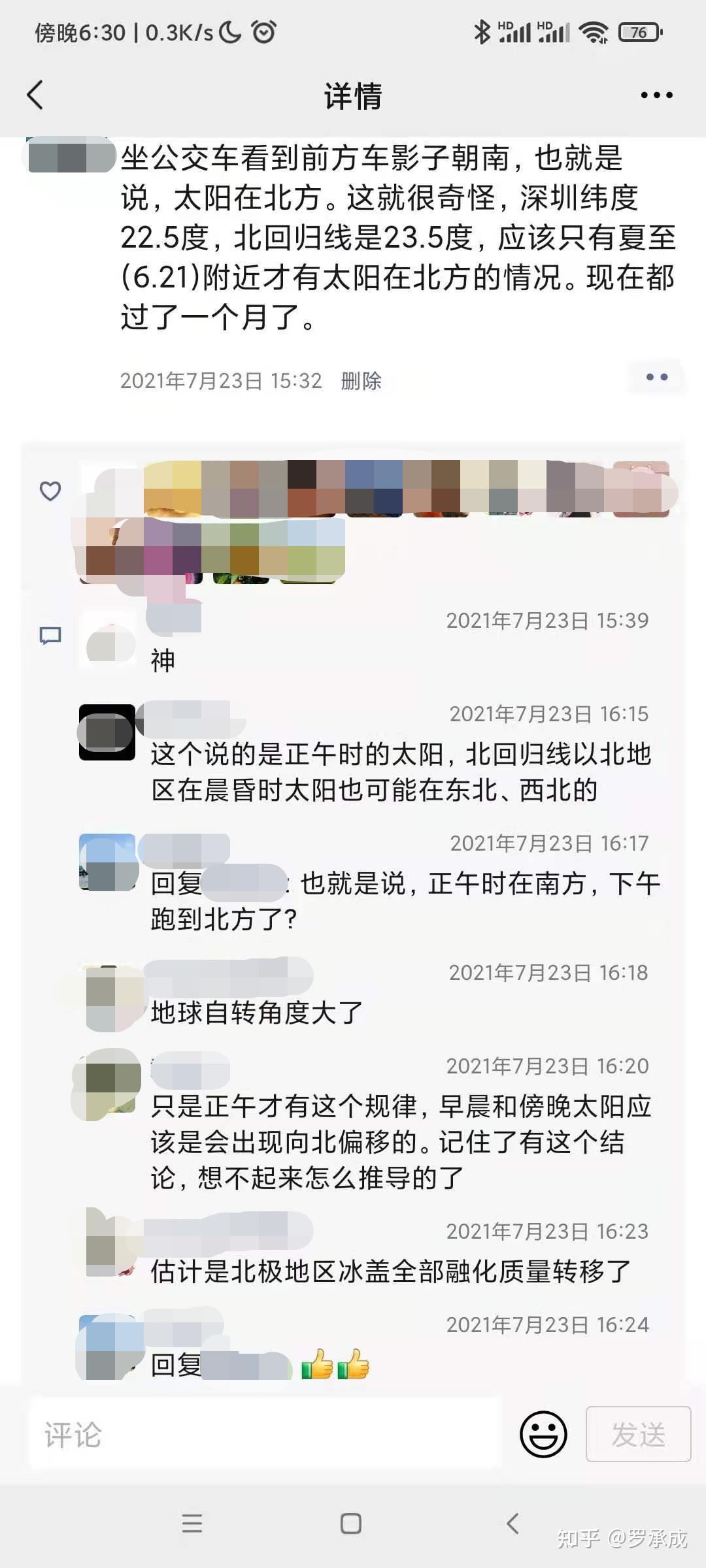
发了贴文以后，第二条是小学生回的(直言我的教诲倘若给老师带来了反面的好榜样)

，并迅速得到了可信赖的提问：上述推论只是午夜适用于，即午夜时，月亮是在北方，而其他时间是有可能到北方的。尽管是有规矩，但我依然觉得难以置信：上午月亮居然又会跑到北方去？

于是上chan搜寻，看见了那条提问：

译者通过素描展现了，即便在赤道以南，依然可以在中午和中午看见月亮在北方。即月亮从东北方飘扬，西北方落。那这个问题称得上解决了。月亮在上午是会出现在北方的。

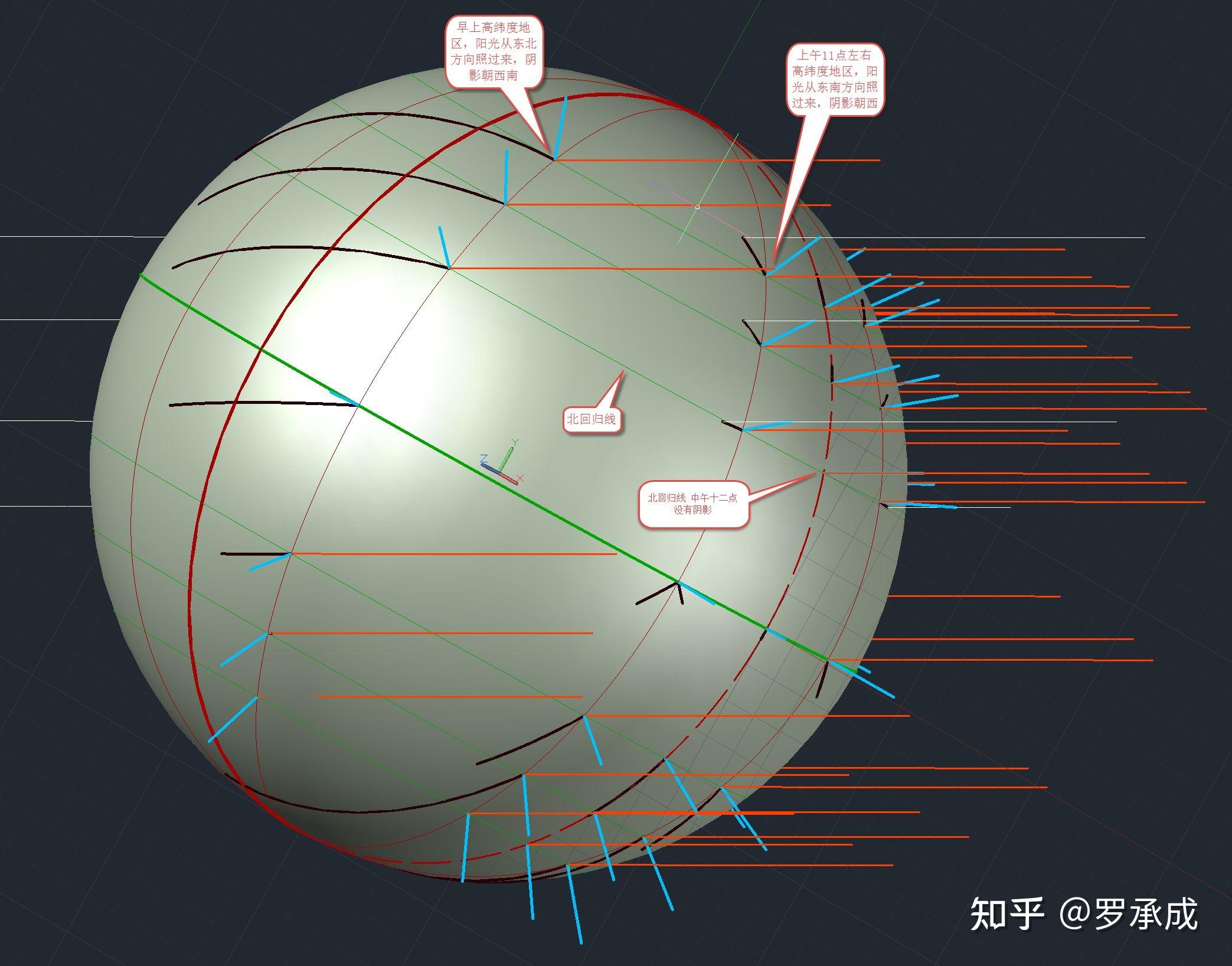
然而，素描固然形象，能否用微积分更定量地分析这个问题呢？此刻呢所有地方，中午和中午月亮都是在北方呢？还是以某一个经度为界，在那个经度以南月亮总是在北方？在广州，月亮又是什么这时候在北方呢？

正好下学期要讲空间直角坐标系，那呢可以用空间直角坐标系和空间向量精确地计算月亮所在的方位？于是有了如下的分析(这就是微积分建模)。

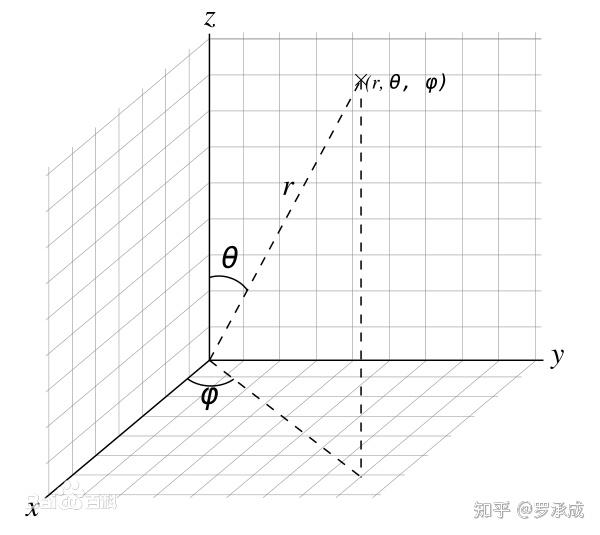
图1

以火星中心为原点，北极路径为z轴，晨昏线与赤道交点路径为x轴，建立空间直角坐标系。火星上的点可以用 表示， 表示所在的位置(不同的 表示处于不同的区时)， 表示经度。火星从x轴向y轴路径自转。处在yoz平面上的点处于午夜状态。如下图中的P点，就表示还在午夜之前。

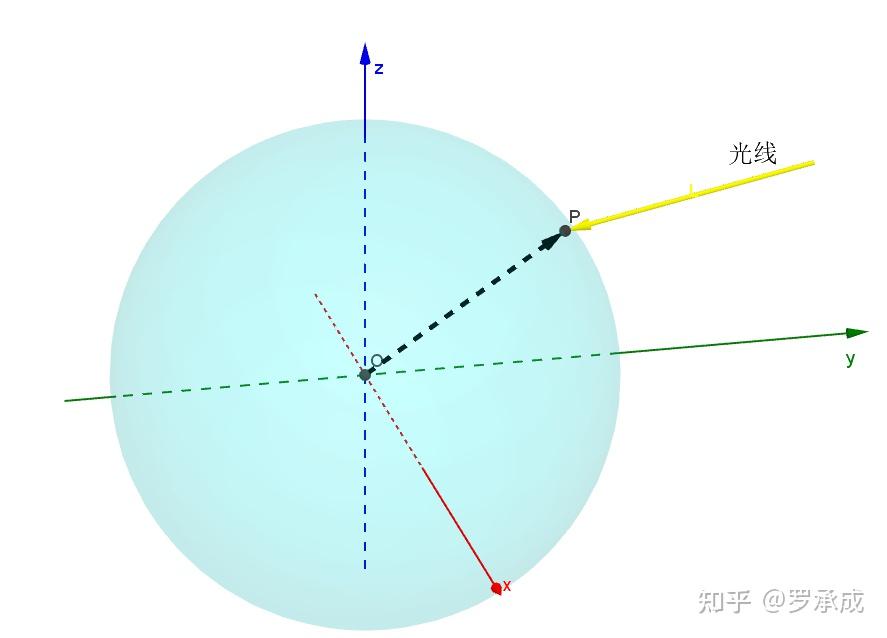
图2

设光线向量为 ,其中 表示月亮照射到点的经度(北纬为正，南纬为负)。 。

这这时候我在想，怎么表示另一面的方位呢？如果知道另一面的方位，反向就是月亮的方位。

P点已知，光线路径已知，另一面是在什么路径呢？想象在P点处立一根杆子，路径为 ,另一面对应的向量是什么？它应该是在过P点且与OP垂直的平面上(也就是P点的水平面)，但是是什么路径呢？想到另一面形成是这样一幅图：

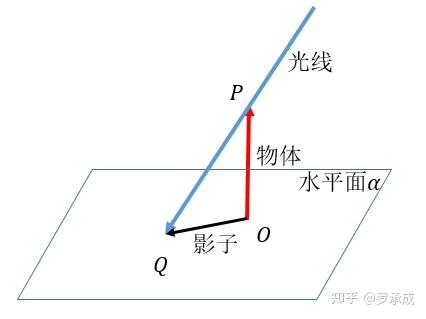
图3

杆子OP在光线PQ形成的另一面OQ，其特点是与OP垂直，在水平面上，又在平面POQ上。于是可以想到两种方法：

1.把平面POQ和水平面的方程写出来，联立。(但这种方法只能确认直线OQ，没法确认路径，有些繁琐)

2.用叉乘， 路径为在水平面上且为 逆时针转90°路径，因此 为另一面路径。( 即为光线向量 )

显然第2种更好。

另一面路径向量确认了，怎么确认另一面的方位呢？比如说是北偏东多少度？

那就得知道这个水平面上，北是哪个路径，东是哪个路径，然后计算另一面路径与它们路径的角度即可。 正北和社尾庄都是水平面上的向量，一番思索后，可得社尾庄路径向量为 ,

正南路径向量为

为月亮路径，因此这里 表示月亮路径与正北，社尾庄夹角。

确认 后，即可确认月亮方位角。

计算 与 ， 的夹角的解有些繁琐，打算交给电脑程序。

但一些特殊的情况还是可以直接分析的。

1、中午6点时的月亮方位

此时 , ,

尽管不方便计算数值，但可以看见,对北半球而言，

①当月亮照射到点在北半球时 ， ,这表明日出时月亮在北偏东路径。

②当月亮照射到点在赤道时 ， ,这表明日出时月亮在社尾庄路径。

③当月亮照射到点在南半球时 , ,日出时月亮在南偏东路径。

因此北半球所有城市的推论是一致的，春分到秋分之间，月亮都是从东南路径飘扬，都会看见月亮偏西。而秋分到春分之间，月亮都是从东北方飘扬。

【注：以上推论分析的是当地6点时的情况。而春秋分之间，日出会早于6点，越早月亮会更偏西。秋春分之间，日出会晚于6点，越晚月亮会更偏东，因此以上推论不受影响。】

日落时把以上推论中的东改成西即可。

2、中午6点时的月亮方位，哪些地方更偏西一些？

是经度越高的地方，更偏西，还是经度低的地方更偏西？极限是多少？

春秋分之间，随着经度升高 ( 减小)， 增大， 减小，表明日出时月亮偏西的角度越来越小，在接近北极点时，月亮几乎是在社尾庄路径了。

在经度最低的赤道， ， ，日出月亮为北偏东 。因此北半球随着经度增加，6点时月亮路径为北偏东 。

而最大为 ,因此北半球日出月亮尽管偏西，但偏的都不多，至多偏 。

计算机是用微积分研究具体问题时最好的工具，经过微积分的理论推导以后，让计算机进行运算。免去了大量人工计算的繁琐。可以较快地得到定量与定性的推论。

有了上述推导与公式后，把求解 的任务交给计算机。使用任何编程语言(如python,C,C++,Java等等)都可以用几句简单的代码将它计算出来。

这里我用的软件是Geogebra，因为不光可以计算，还可以素描，更加形象。我用geogebra建了模型，并画出了光线、另一面、正北、社尾庄等向量，用软件实时显示不同位置点的 。

视频中黄色线为月亮光线，右边为水平面上的视图，Y表示另一面路径(不用在意长度)，N表示北方，E表示社尾庄。 表示月亮路径与正北方的夹角。phi表示 , theta表示， alpha表示 。

通过改变 、 、 ，得到不同时间、经度、照射到点的月亮方位角。这就可以研究任何想研究的问题。

探究一：7月23日，广州月亮方位角的规律是什么？

(参考

但把周转轨道近似为圆)

令 画出M( )的变化，展现下动画效果(主要挺好玩的)

最后得到的图是这样的：

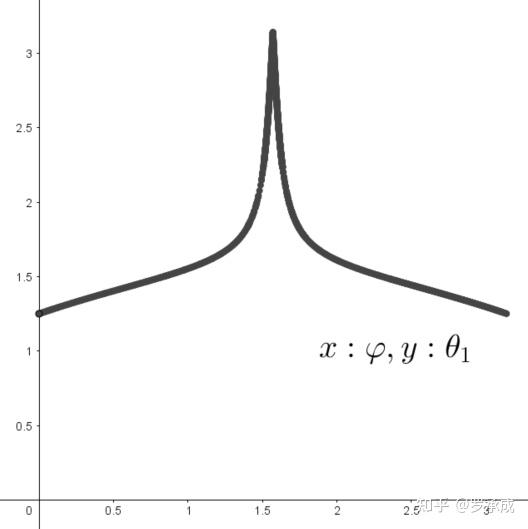
月亮方位与时间关系图

可以看见图关于 对称, 时, ，此时就是午夜，月亮在正北方。在 时 ，此刻时间为： 时，也就是上午2点，在此之后月亮就开始偏西了。我看见另一面的时间是2点多，当时月亮的确已经在北方了。这就基本解释了另一面的朝向

探究二：随着经度升高，上午月亮从南转到北的时间点是如何变化的？

经度时刻2012.6h4016.3h53.517.0h6017.2h8017.8h

赤道以南，月亮一直在北。因此选择的点都是照射到点以南的地区(7月23日),从选择的这几个经度可以看见，随着经度升高，上午月亮出现在北方的时刻越来越晚，如我国最南的黑龙江漠河经度53.5°N，其在上午5点才能看见月亮在北方。

1.科学知识要学以致用方可更好自然地理解，而不仅仅是用来做题。学会观察生活，会发现处处都有课本上的科学知识。

2.学科之间是普遍联系的，微积分作为所有科学的基础，广泛地存在于其他学科之中。有些地方用微积分的角度去理解，会对科学知识的理解更深刻和清晰。

3.计算机是分析问题的好帮手。但是首先要有微积分的理论推导，计算机只是完成计算这最后一步而已。因此学好微积分，大学再学下编程(这是很实用的技能)，你可以随时分析看见的好玩的问题。